Les fonctions de hachage sont des fonctions particulières très utilisées dans le cadre de la sécurité informatique, notamment dans le domaine de la cryptographie et des certificats numériques. Elles permettent d’obtenir une empreinte, également appelée condensat (« hash »), à partir d’un message ou de tout document numérique.

Il existe un nombre assez restreint de fonctions de hachage, car elles sont assez complexes à mettre au point et reposent sur des mécanismes mathématiques complexes.

Principales caractéristiques

En pratique

Une fonction de hachage est une fonction mathématique particulière permettant de calculer rapidement l’empreinte d’une donnée informatique. Une fonction de hachage doit présenter les caractéristiques suivantes :

• La taille du condensat (« hash ») est fixe (pour un algorithme donné) ;
• Elle ne fonctionne que dans un sens (c’est-à-dire qu’il n’existe pas de fonction inverse) ;
• Pour une entrée donnée, on doit toujours obtenir le même résultat (empreinte) ;
• Toute modification même très légère en entrée produit un résultat très différent ;
• Elle est rapide à calculer.

L’intérêt de ce condensat est d’avoir une sorte de signature d’un document :

• L’irréversibilité permet de ne pas pouvoir retrouver le document original à partir du condensat (il est même très difficile de construire un document quelconque à partir d’une empreinte donnée) ;
• Si deux hashs sont différents, alors les documents initiaux sont forcément différents.

Intérêt et usage des fonctions de hash

L’intérêt principal est de permettre d’identifier la donnée de façon presque sûre sans pour autant transmettre la donnée : il est mathématiquement très difficile (voire impossible) de retrouver la donnée initiale à partir de son empreinte.

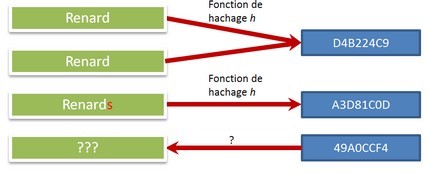
Ces fonctions peuvent avoir plusieurs usages, plus ou moins critiques. Cela peut aller du simple contrôle technique pour s’assurer qu’un message a été correctement transmis (ou n’a pas été modifié), jusqu’à la signature électronique.

Pour le mot de passe

On s’en sert également pour chiffrer les mots de passe dans beaucoup de systèmes. Puisque ces fonctions sont rapides, on peut facilement calculer l’empreinte d’un mot de passe ; c’est alors lui qui est stocké dans le système, et non le mot de passe en clair. Comme il est difficile de retrouver la donnée initiale à partir d’une empreinte, la protection ainsi obtenue est bonne (plus ou moins en fonction de l’algorithme utilisé et de sa mise-en-oeuvre).

Lorsqu’un utilisateur veut se connecter à un système, il entre son mot de passe. On calcule ensuite son empreinte : si c’est la même que celle stockée dans le système, l’accès est alors autorisé.

Pour vérifier l’intégrité d’une donnée

Si on souhaite vérifier qu’une donnée (un fichier informatique) est intègre, c’est-à-dire non modifiée, on communique le fichier au destinataire et ce dernier recalcule lui-même son empreinte : celle-ci doit correspondre à une empreinte de référence.

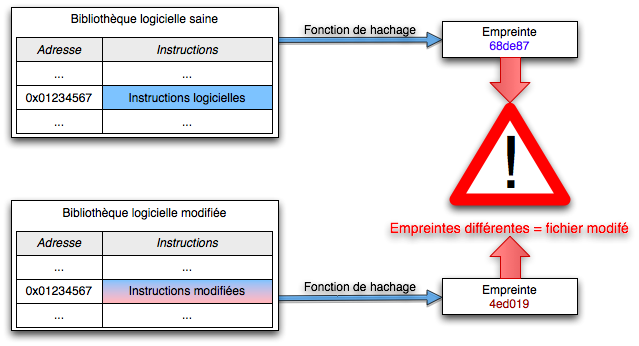
Toute la subtilité vient ensuite de la façon dont on connaît cette empreinte de référence : quand on télécharge un fichier, cela peut être une somme de contrôle ; pour un certificat, c’est une des données du certificat.

Pourquoi presque sûre ?

L’empreinte est généralement de petite taille et de longueur fixe. Même si cela représente beaucoup de possibilités, ce nombre est fini, alors que le nombre d’entrées possibles est, lui, infini.

Statistiquement, il est donc très peu probable que deux données différentes en entrée produisent la même empreinte, mais c’est possible : la difficulté augmente avec la longueur choisie pour l’empreinte. Pour SHA-1, c’est 160 bits. pour SHA-256 c’est… 256 bits !

Trouver deux données différentes ayant un même hash est appelé collision. La probabilité d’une collision dépend principalement de la longueur du hash, mais aussi (un peu) de la façon dont il est calculé (notamment la rapidité de son calcul).

Les propriétés et les attaques

Propriétés formelles attendues d’une fonction de hachage

Reprenons un peu le chemin de la théorie. Selon McAfee Labs (Intel)¹, une bonne fonction de hachage doit avoir les propriétés suivantes :

• Résistance à la préimage : Pour une valeur de hachage donnée, il doit être difficile de trouver un fichier ou message pour lequel la fonction de hachage produirait une valeur identique.
• Résistance à la seconde préimage : Pour un fichier ou message donné, il doit être difficile de trouver un second fichier ou message tel que la fonction de hachage produirait la même valeur pour les deux fichiers ou messages.
• Résistance à la collision : Il doit être difficile de trouver deux fichiers ou messages distincts pour lesquels la fonction de hachage produirait la même valeur de hachage.

Dis comme ça, il n’est pas évident de voir la différence (je parle pour moi). Mais l’enjeu de cette formalisation est de voir quels sont les types d’attaques possibles : chaque propriété est plus ou moins forte, pour un type de hash donné. Et plus la propriété est faible, plus une attaque est probable.

Les différents type d’attaques

Attaques par collision

Il existe deux types principaux d’attaques de collisions :

• l’attaque de collisions classique : cette attaque consiste à trouver deux messages m1 et m2 différents, tels que hachage (m1) = hachage (m2) ;
• l’attaque de collisions avec préfixes choisis : étant donné deux préfixes différents P1 et P2, cette attaque consiste à trouver deux suffixes S1 et S2 tels que hachage (P1 ∥ S1) = hachage ( P2 ∥ S2) (où ∥ est l’opération de concaténation).

Source : Wikipédia

xxx

Qu’est-ce qui se passe avec SHA-1

Il se passe que la robustesse de SHA-1 est remise en question face au développement de la puissance de calcul disponible. Or SHA-1 est très utilisé, notamment pour les certificats ; or si on peut attaquer SHA-1, on peut alors attaquer des certificats et créer des faux !

Pour plus d’informations : voir SHA-1.

Ce qu’affichent les navigateurs

La signalétique est généralement univoque. Chrome affiche du vert quand c’est sûr, du gris pour un avis neutre, et du rouge quand le niveau de sécurité est trop faible.

Malheureusement tout le monde applique un peu les règles qu’il veut, comme il le sent, ce qui aboutit à des incohérences pour un utilisateur multi-navigateurs (comme moi). Google a tendance à avoir l’attitude la plus restrictive, ce qui n’est pas forcément condamnable, sauf que cela n’a pas toujours de l’intérêt, comme par exemple sur des sites de peu d’influence ou de peu d’importance.

De plus, Google change ses règle si rapidement qu’un utilisateur peut être perdu en voyant un site « dégradé » (en termes de sécurité) d’une version à l’autre du navigateur.

Exemple d’utilisation

Sous Linux, si vous ne disposez pas des commandes shaxxxsum :

openssl dgst -sha1 filename

References